Depth-First Search Variations and A*
Best-First Search as a Generalized Search Algorithm
Breadth-first search:
Depth-first search:
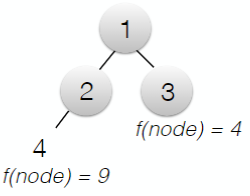
Which frontier node would we visit first?
The one with the lowest estimated solution cost, given an evaluation function f: node
The function f can be chosen so as to lead to informed search algorithms.
1. Informed (Heuristic) Search
- Informed search algorithms make use problem-specific knowledge that goes beyond the problem formulation, in an attempt to improve efficiency.
- Heuristic functions are the most common form of using such knowledge in search algorithms.
- A heuristic is a function h: node
estimate the cost of the cheapest path from the state at the node to a goal state. - Heuristics are hints / rules of thumb: approximate, quick to compute, not guaranteed to work.
- Can be used to guide the search and cut down the number of node expansions before finding a goal.
- How much more efficient the search will be in comparison to uninformed search depends on the quality of the heuristic.
- A heuristic is a function h: node
2. A* Search
1. Introduction
A widely known best-first informed search algorithm. Works for problems where the cost of actions may differ.
Evaluation function:
where
2. Algorithm for
- Visit the node with the smallest
first, placing each child in the frontier. - Do not place the child in the frontier if its corresponding state is already in the list of visited nodes.
- If the state of a given child is already in the frontier:
- If the frontier node has a larger
, place the child to the frontier and remove the larger node from the frontier. - Else, do not place the child in the frontier.
- If the frontier node has a larger
- Stop when you visit a node which is a goal node.
3. Consistency (Monotonicity)
When using a consistent heuristic, A* is complete and optimal, i.e., guaranteed to find an optimal solution if one exists.
4. Generating Heuristics
- Heuristics are problem dependent, and can be difficult to devise.
- Hint: generate a heuristic based on a relaxed version of the problem, i.e., a problem with fewer restrictions on actions.
Hill-Climbing
1. Artificial Intelligence Optimization Algorithms
- Advantages:
- Usually more space efficient, frequently requiring constant space.
- They do not maintain paths to solutions.
- Frequently able to find reasonable solutions for problems with large state spaces, for which the tree-based search algorithms are unsuitable.
- Can potentially be more time efficient, depending on the algorithm.
- Do not necessarily require problem-specific heuristics.
- Usually more space efficient, frequently requiring constant space.
- Weaknesses:
- Not guaranteed to retrieve the optimal solution.
- Depending on the problem formulation and operators, not guaranteed to be complete either.
- Applicability:
- Can be used for any problem that can be formulated as an optimization problem.
3. Optimization Problems
- Optimisation problems: to find a solution that minimises/ maximises one or more pre-defined objective functions.
- Maximisation / minimisation problems.
- What constitutes a solution depends on the problem in hands.
3. Traveling Salesman Problem Formulation
Design variables represent a candidate solution.
- Sequence x containing N cities to be visited.
Design variables define the search space of candidate solutions.
- All possible sequences of cities.
[Optional] Solutions must satisfy certain constraints, which define solutions feasibility.
- Each city must appear once and only once in x (explicit constraint).
- Salesman must return to the city of origin (implicit constraint).
Objective function defines the quality (or cost) of a solution.
Total_distance(x) =
sum of distances between consecutive cities in x +
distance from last city to the origin
To be minimized.
4. Hill-Climbing
Hill-Climbing (assuming maximization)
- current_solution = generate initial candidate solution randomly.
- Repeat:
- generate neighbor solutions (differ from current solution by a single element)
- best_neighbor = get highest quality neighbor of current_solution
- If quality (best_neighbor) <= quality (current_solution)
- Return current_solution
- current_solution = best_neighbor.
Illustrative Example
- Design variables represent a candidate solution.
- x ∈ Z
- Design variables define the search space of candidate solutions.
- Our search space are all integer numbers.
- [Optional] Solutions must satisfy certain constraints, which define solution feasibility.
- None
- Objective function defines the quality (or cost) of a solution.
, to be maximized
- Representation
- Integer variable
- Initialization
- Initialize with an integer value picked randomly.
- Neighborhood
- Add or subtract 1.
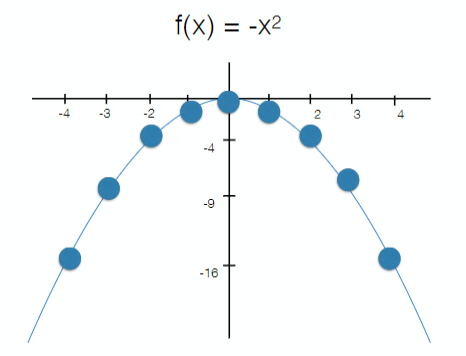

5. Greedy Local Search
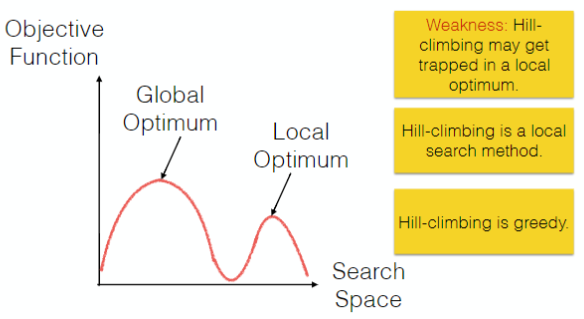
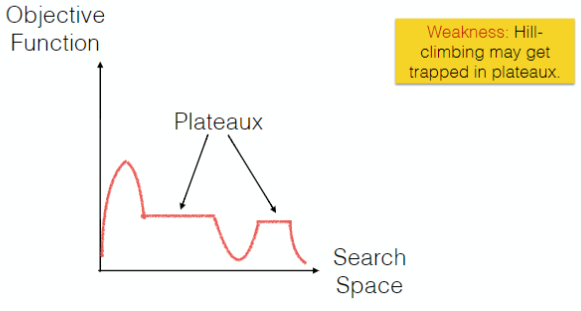
The success of hill-climbing depends on the shape of the objective function for the problem instance in hands.
Hill-climbing has been successfully applied to software module clustering.