Basic Set Theory
Set
no duplicate element. Subset
. A is a subset of B if every element in A is contained in B Proper Subset
. Set A is said to be a proper subset of B if every element in A is contained in B AND . Union
. The Union of two sets A and B is the set that contains all the elements from A and B. Intersection
. The Intersection of two sets A and B is the set that contains elements from BOTH A and B. Set difference / Set minus
. The Set difference between A and B is the set of all members in A that are not in B. Symmetric difference
. The Symmetric difference of sets A and B, consists of the set containing elements contained in exactly one of A or B. Example:
. Ordered pair / Tuple
. An ordered pair is a pair of elements whose order is maintained. Example: A tuple is a list of elements:
. Cartesian product
. The Cartesian product of A and B, is the set whose members are all possible ordered pairs (a, b) where a is a member of A and b is a member of B. Example:
. Element of
. Elements of a set. Universal set
. The universal set is a set which contains all objects, including itself. Null set
. The null set is the set that contains no elements.
SQL
1. SQL Relations
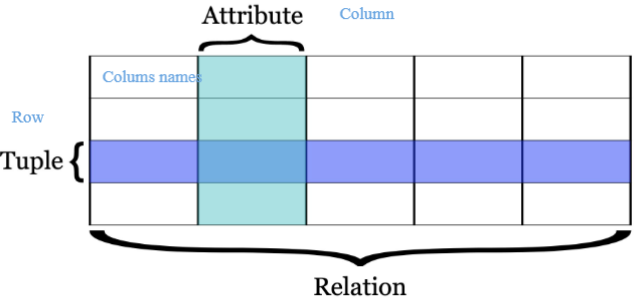
2. SQL Language
There are two parts to the Language:
Data Definition Language (DDL)
Create and Delete "tables"
Data Manipulation Language (DML)
Query information
Insert information
Update, Delete
Other commands include "index", "view", ...
1. SQLBolt
SQLBolt: A nice website that can help you go through all operations including subqueries and set operations.
2. w3schools.com
SQL Tutorial: More detailed than the website above. Including caseand wildcard.
Entity Relationship Diagrams
Elements of Database Design
- Conceptual Modelling
- Logical Design of the Database
- Distributed Database Design
- Physical Database Design
Entity Relationship Diagrams
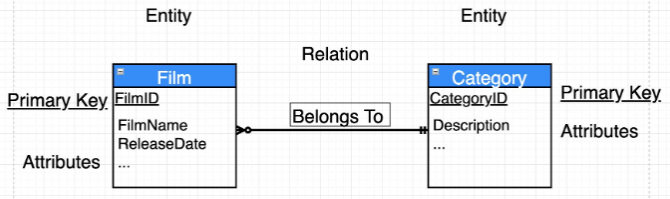
ERDs have an Language Correspondence. Attributes associated with an Entity are listed within the rectangle. The primary attribute (which uniquely identifies an entity) is underlined. Relations are NAMED associations between Entities. Relationships provide associations in BOTH directions.
1. Cardinality
This provides constraints on the number of entities that participate in a relationship.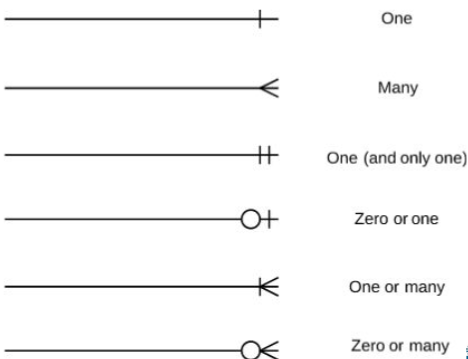 
2. Weak Entities
These are entities that do not have a primary key. They must borrow a part or all of it from another entity. eg. Building 1 have 101 room, building also could also have 101 room.
An Identification Relationship provides ONE component of a Weak Entity's Primary Key. An Identifying Dependency consists of one or more Identification Relationships to provide ALL of a Weak Entity's Primary Key. Sometimes, they are equivalent.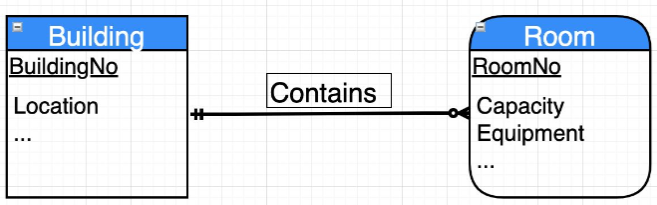 
Weak Entities are represented using rounded rectangles. The underlined attribute is NOT the primary key, but is a key which when added to the key of one or more entities provides a primary key.
Converting to Tables:
The primary key of a Weak Entity consists of the combination of the Key of that entity and Foreign keys of one or more other Entities.
3. Many to Many Relations
There are several instances where many elements of one entity are associated with many elements of another.
In Many to Many relationships, relationships can have attributes.
Examples: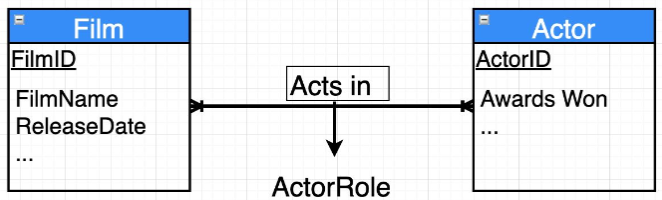 
You can replace a many to many relationship (n-m) with:
An Associate Entity
TWO one to many relations
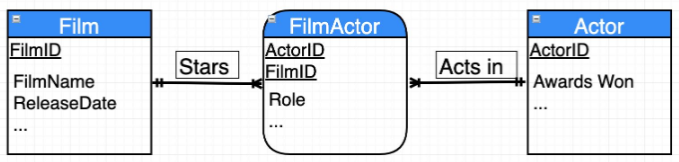
Associative Entities provide additional information about the many to many association between entities. They are necessarily Weak Entities, borrowing their primary key from the entities they provide an association between.
4. N-Way Relations
Sometimes - very rarely - more than two entities are related to each other. We use an N-Way relation iff we need to record information associated with 3 or more entities.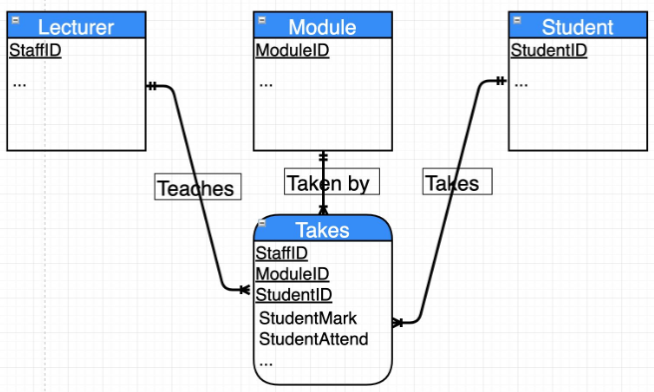 
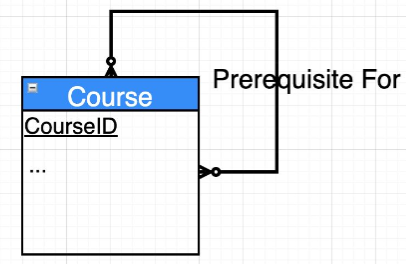
5. Self Identifying Relations
Self Identifying OR Self Referencing OR Reflexive relationships are relationships between an Entity and itself.
Example: Many to One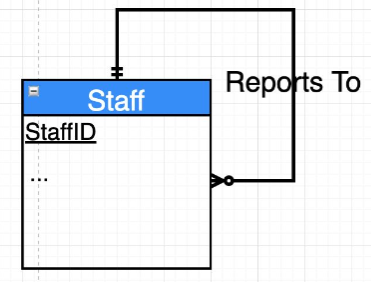 
Example: Many to Many 