Biantian's Studio.

DS 06

DS hashtable
Word count: 699Reading time: 4 min
2020/04/15 Share

Hash tables & Graphic

Hash Tables

1. Summary

A hash table consists of

  1. an array arr for storing the values.
  2. a hash function hash(key).
  3. a mechanism for dealing with collisions.

Basic operations

  1. put(key, value)
  2. delete(key)
  3. get(key)

Disclaimer: We will consider a simplified situation where keys and values are the same. For example, an assignment is always:

arr[hash(key)] = key.


2. Two types of solutions of hash collisions

1. Sticking out strategy

2. Tucked in strategy

Linear Probing

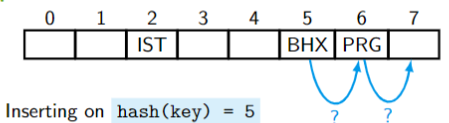
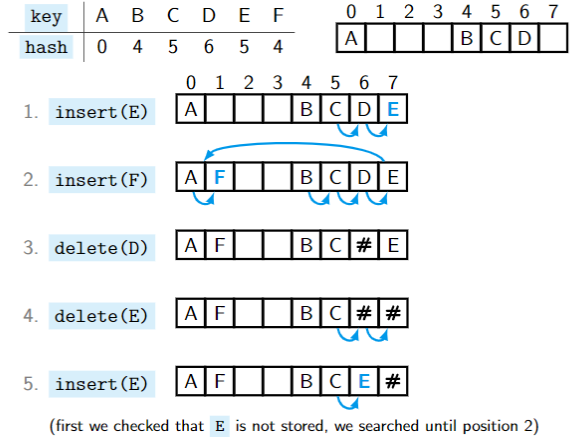
  • Insertion (initial idea): If the primary position hash(key)is occupied, search for the first available position to the right of it. If we reach the end, we wrap around.

  • Deletion:

    1. Find whether the key is stored in the table: Starting from the primary position hash(key), go the right, until the key or an empty position is found.

    2. If the key is stored in the table, replace it with a tombstone (marked as #).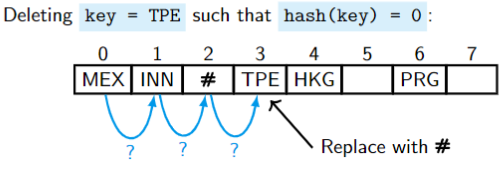

  • Searching:

    Starting from the primary position hash(key), search for the key to the right. We skip over all tombstones #. If we reach an empty position, the the key is not in the table.

  • Inserting (more accurately):

    1. check if key is stored in the table , and
    2. if it is not and its the primary position hash(key) is occupied by a different key, search for the first empty or tombstone position to the right of it.
    3. Store the key there.


Double hashing

To deal with the problem caused by Primary clusters, we need to use double hashing.

Use primary and secondary hash functions hash1(key) and hash2(key), respectively.

  • Insertion: We try the primary position hash1(key) first and, if it fails, we try fallback positions:

    (hash1(key) + i*hash2(key)) % TABLE_SIZE (until we find an available space).

Avoiding short cycles

  1. T is a prime number.
  2. and hash2(key) is always an odd number. (preferred)


3. Time Complexity

The load factor of a hash table is the average number of entries stored on a location:

n = the total number of stored entries, T = the size of the hash table. If we have a good hash function, a location given by hash(key) hash the expected number of entries stored there equal to .

3. What to do if the table is full?

We say that a hash table is full if the load factor is more than the maximal load factor, that is,

Rehashing (idea): If the table becomes full after an insertion, allocate a new twice as big table and insert all elements from the old table into it.


Graphs and graph algorithms

A graph is formed of a (finite) set of vertices/nodes and a set of edges between them. We distinguish four types of graphs: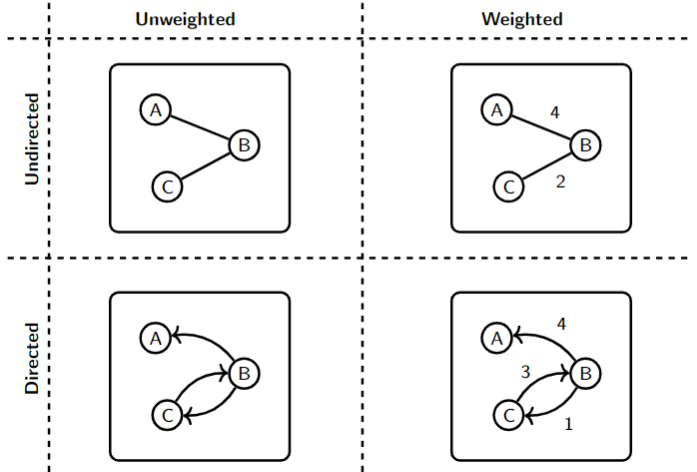

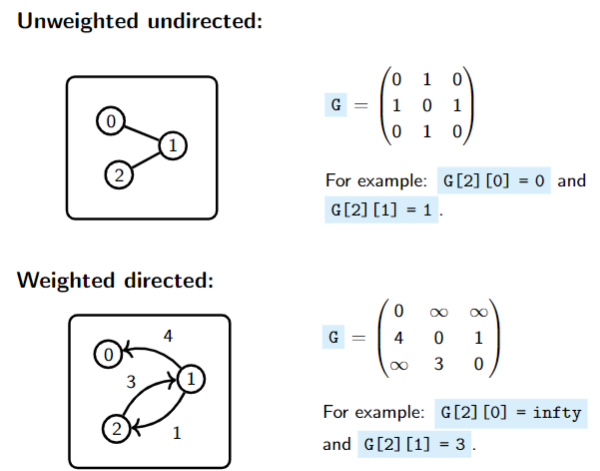
1. Adjacency Matrix

Assume that graph's vertices are numbered .

Adjacency matrix G is a two-dimensional array/matrix described as follows:

  • Unweighted graphs:
    • G[v][w] = 1 if there is an edge going from v to w
    • G[v][w] = 0 if there is no such edge
  • Weighted graphs:
    • G[v][w] = weight of the edge going from v to w
    • G[v][w] = if there is no such edge
    • G[v][w] = 0
  • Remark: The graph is undirected if G[v][w] = G[w][v] for all vertices v and w.

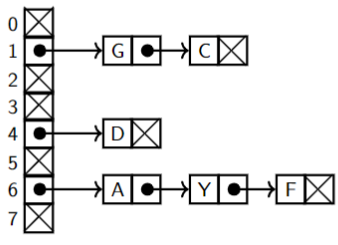
2. Adjacency List

To represent a graph on vertices by adjacency lists we have an array N of n-many linked lists (one list for every vertex).

  • Unweighted:
    • N[v] is the list of neighbors of v. (w is a neighbor of v if there is an edge )
  • Weighted directed:
    • N[v] is the list of neighbors of v together with the weight of the edge that connects them with v.

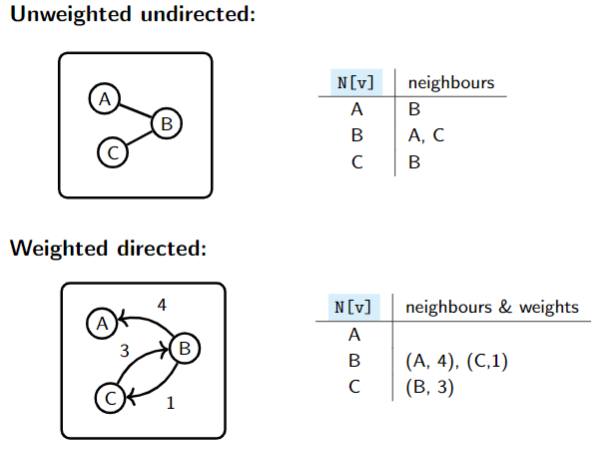
For example, N[2] stores the address of the head of the linked list of all neighbors of the 2nd vertex.

3. Comparison


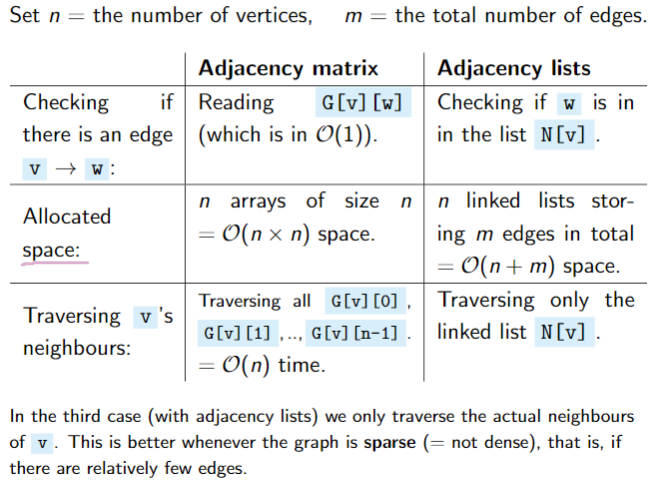
4. Paths and shortest paths

1. Definition

A path from v to z is a sequence of edges connecting v with z.

The shortest path is the path such that the sum of weights of its edges is the minimal. (In unweighted graphs, set weights to 1.)

2. Dijkstra's algorithm

View Youtube.

3. Prim's algorithm

View Youtube.

Author：Biantian

原文链接：http://biantian.github.io/2020/04/15/ds6/

发表日期：April 15th 2020, 2:58:55 am

更新日期：April 15th 2020, 9:52:51 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Hash tables & Graphic
    1. 1.1. Hash Tables
      1. 1.1.1. 1. Summary
      2. 1.1.2. 2. Two types of solutions of hash collisions
        1. 1.1.2.1. 1. Sticking out strategy
        2. 1.1.2.2. 2. Tucked in strategy
          1. 1.1.2.2.1. Linear Probing
          2. 1.1.2.2.2. Double hashing
        3. 1.1.2.3. 3. Time Complexity
      3. 1.1.3. 3. What to do if the table is full?
    2. 1.2. Graphs and graph algorithms
      1. 1.2.1. 1. Adjacency Matrix
      2. 1.2.2. 2. Adjacency List
      3. 1.2.3. 3. Comparison
      4. 1.2.4. 4. Paths and shortest paths
        1. 1.2.4.1. 1. Definition
        2. 1.2.4.2. 2. Dijkstra's algorithm
        3. 1.2.4.3. 3. Prim's algorithm
Total : 12
2020
AI DB DS hashtable OSN hexo web note
Revision