Biantian's Studio.

DS 04

DS
Word count: 413Reading time: 2 min
2020/04/14 Share

Priority Queues

(Max) Priority Queue = Max-In-First-Out

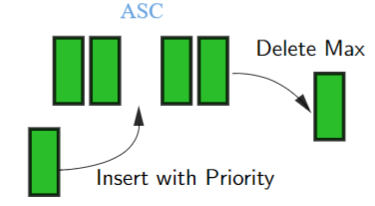
1. Basic Operations

  • insert(value,priority)
  • deleteMax()
  • update(value,priority)
  • isEmpty()

2. Naïve implementation: Array

Store in an array, ordered by priority (the highest at the end):

  • insert(value, priority) - find the position where to store the element, shift to the right the elements starting from that position 1.
  • deleteMax() - return the last stored element .

3. Better implementation: Binary Heaps

3.1 Definition

Invariants of heap trees are as follows:

  1. The priority of every node is higher than (or equal to) that of its children.
  2. All levels are completely filled, except possibly the last one, which is partially filled from the left.

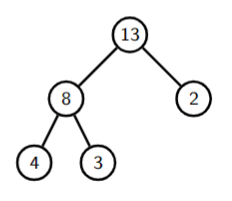
3.2 Insertion

Insert the value at the end of the last level and then keep bubbling it up as long as it is larger than its parent.

Inserting p to a heap which already has n elements stored in it (pseudocode):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void insert(int p, int[] heap, int n){
    if(n==MAXSIZE)
        throw HeapFullException;
    n = n + 1;
    heap[n] = p;
    bubbleUp(n, heap, n);
}
void bubbleUp(int i, int[] heap, int n){ // i -> index
    if(i == 1) return;
    if(heap[i] > heap[parent(i)]){
        swap heap[i] and heap[parent(i)];
        bubbleUp(parent(i),heap,n);
    }
}

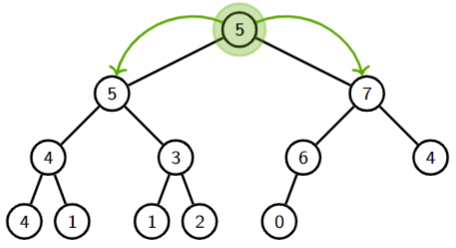
3.3 Delete Max

  1. Make the last node in the last level the new root.
  2. Then bubble down: keep swapping it with the higher priority child as long as any of its children has a higher priority.

pseudocode:

1
2
3
4
5
6
7
8
9
10
11
int deleteMax(int[] heap, int n){
    if(n<1)
        throw EmptyHeapException;
    int result = heap[1];
    heap[1] = heap[n];
    bubbleDown(1,heap,n-1);
    return result;
}
void bubbleDown(int i, int[] heap, int n){
	// omitted
}

3.4 Storing heap trees in arrays

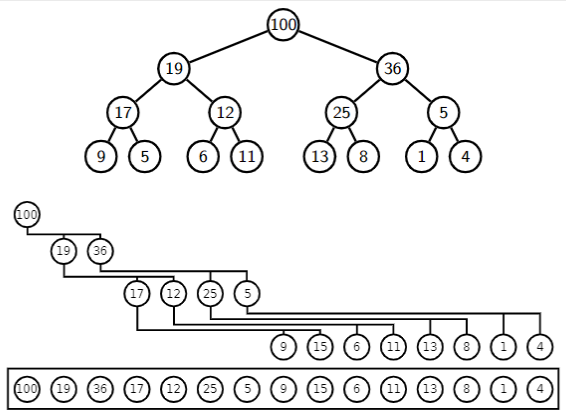
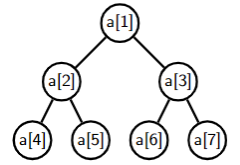
If we start counting from 1. The root node is stored on position 1.

or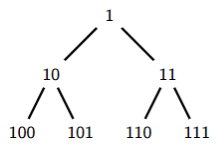

For a node stored on position i.

  1. its left child is on position 2*i.
  2. its right child is on position 2*i + 1.
  3. its parent is on position i div 2.

3.5 Heapify

Method 1:

Can insert entry by entry and bubble up each time, total .

Method 2:

Simply fill the array and bubble down each entry. This is . Start bubble down from the last node of penultimate line, because the nodes in last line don't need it.

1
2
3
4
5
void heapify(int[] arr, int n){
    for(int i = n div 2; i>0;i--){
        bubbleDown(i, arr, n);
    }
}

  1. View List of mathematical symbols↩

Author：Biantian

原文链接：http://biantian.github.io/2020/04/14/ds4/

发表日期：April 14th 2020, 3:14:17 am

更新日期：April 14th 2020, 4:41:10 am

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. Priority Queues
    1. 1.1. (Max) Priority Queue = Max-In-First-Out
      1. 1.1.1. 1. Basic Operations
      2. 1.1.2. 2. Naïve implementation: Array
      3. 1.1.3. 3. Better implementation: Binary Heaps
        1. 1.1.3.1. 3.1 Definition
        2. 1.1.3.2. 3.2 Insertion
        3. 1.1.3.3. 3.3 Delete Max
        4. 1.1.3.4. 3.4 Storing heap trees in arrays
        5. 1.1.3.5. 3.5 Heapify
Total : 12
2020
AI DB DS hashtable OSN hexo web note
Revision